Skip to main content

​
Future Leaked Covariate Importance in Synthefy Foundation Model using Zero-Perturbation Analysis

In this walkthrough, we demonstrate how to estimate the influence of leaked covariates by zero-perturbing them only at inference time. In this work, we generate synthetic autoregressive-with-exogenous-input (ARX) time-series data and demonstrate that Zero-Perturbation Analysis appropriately assigns scores based on the usefulness of the data. We show how to:
  • βœ… Run a perturbation experiment using sMAPE
  • βœ… Visualize how forecasts change when each covariate is removed
  • βœ… Aggregate importance across 100 simulation runs

​
πŸ” Goal

Which external covariates does the model actually rely on for forecasting?
The core tool we utilize is Zero-Perturbation Analysis: for each covariate, mask the entire covariate, both history and future leaked, by replacing it with zero, and compare the prediction error (sMAPE) for this data point. If the model depends heavily on a covariate, removing it will hurt the forecast.

​
πŸ§ͺ 1) Synthetic ARX Data

We simulate data from an ARX(3,4) model with four exogenous inputs: yt=0.5ytβˆ’1+0.3ytβˆ’2+0.1ytβˆ’3+0.8x1,t+0.5x2,t+0.9x3,t+0.2x4,t+Ξ΅t,y_t = 0.5 y_{t-1} + 0.3 y_{t-2} + 0.1 y_{t-3} + 0.8 x_{1,t} + 0.5 x_{2,t} + 0.9 x_{3,t} + 0.2 x_{4,t} + \varepsilon_t, with Gaussian noise Ξ΅t∼N(0,0.12)\varepsilon_t \sim \mathcal{N}(0, 0.1^2). This is a linear function of the history and the exogenous inputs, which are sampled from random Fourier functions with orders between 3-20. Note that we can generate a near-infinite variety of ARX(3,4) time series by sampling different exogenous inputs. Output columns:
ColumnDescription
yttarget time series
x1–x4exogenous inputs (MixedSampler)
timeinteger index (optional)

​
βš™οΈ 2) Prepare History / Forecast Split

We split the series into history and forecast horizon (default 80/20). 
import pandas as pd

TARGET_COL = "target"     # rename for downstream
TIMESTAMP_COL = "timestamp"

# Convert to standard format
df = df.rename(columns={"yt": TARGET_COL})
df[TIMESTAMP_COL] = pd.date_range("2020-01-01", periods=len(df), freq="D")

# Identify covariates (everything except timestamp/target/time)
exclude = {TIMESTAMP_COL, TARGET_COL, "time"}
metadata_cols = [c for c in df.columns if c not in exclude]

cut = int(len(df) * 0.8)
history_df = df.iloc[:cut].copy()
future_df = df.iloc[cut:].copy()
ground_truth_df = future_df.copy()

​
🧯 3) Zero-Perturbation Protocol & sMAPE Shift

For each covariate xjx_j, we zero it over both the history and forecast horizon (no retraining) and measure the relative sMAPE shift as a percentage: Ξ”j=100β‹…sMAPE(y,y^(j))βˆ’sMAPE(y,y^base)sMAPE(y,y^base)\Delta_j = 100 \cdot \frac{\mathrm{sMAPE}(y, \hat y^{(j)}) - \mathrm{sMAPE}(y, \hat y^{\mathrm{base}})} {\mathrm{sMAPE}(y, \hat y^{\mathrm{base}})} Intuitively, this metric indicates how much the performance dropped relative to the overall accuracy of the prediction, an indicator for how important the covariate is. 
# perturbation_analysis_arx.py (core call)
from perturbation_analysis import run_analysis  # your existing helper

results, baseline_forecast, perturbed_forecasts = run_analysis(
    history_df=history_df,
    future_df=future_df,
    ground_truth_df=ground_truth_df,
    target_col=TARGET_COL,
    timestamp_col=TIMESTAMP_COL,
    metadata_cols=metadata_cols,  # ['x1','x2','x3','x4']
    leak_cols=metadata_cols,      # treated as known exogenous for forecasting
)

# results: per-covariate Ξ”-sMAPE (%), baseline smape, etc.
print(results)
Interpretation:
  • Ξ”j>0\Delta_j > 0: removing xjx_j hurts accuracy β†’ model depends on it
  • Ξ”j≀0\Delta_j \le 0: removing xjx_j helps or does nothing β†’ likely redundant/noisy

​
πŸ“Š 4) Single-Run β€œSummary” Plots

​
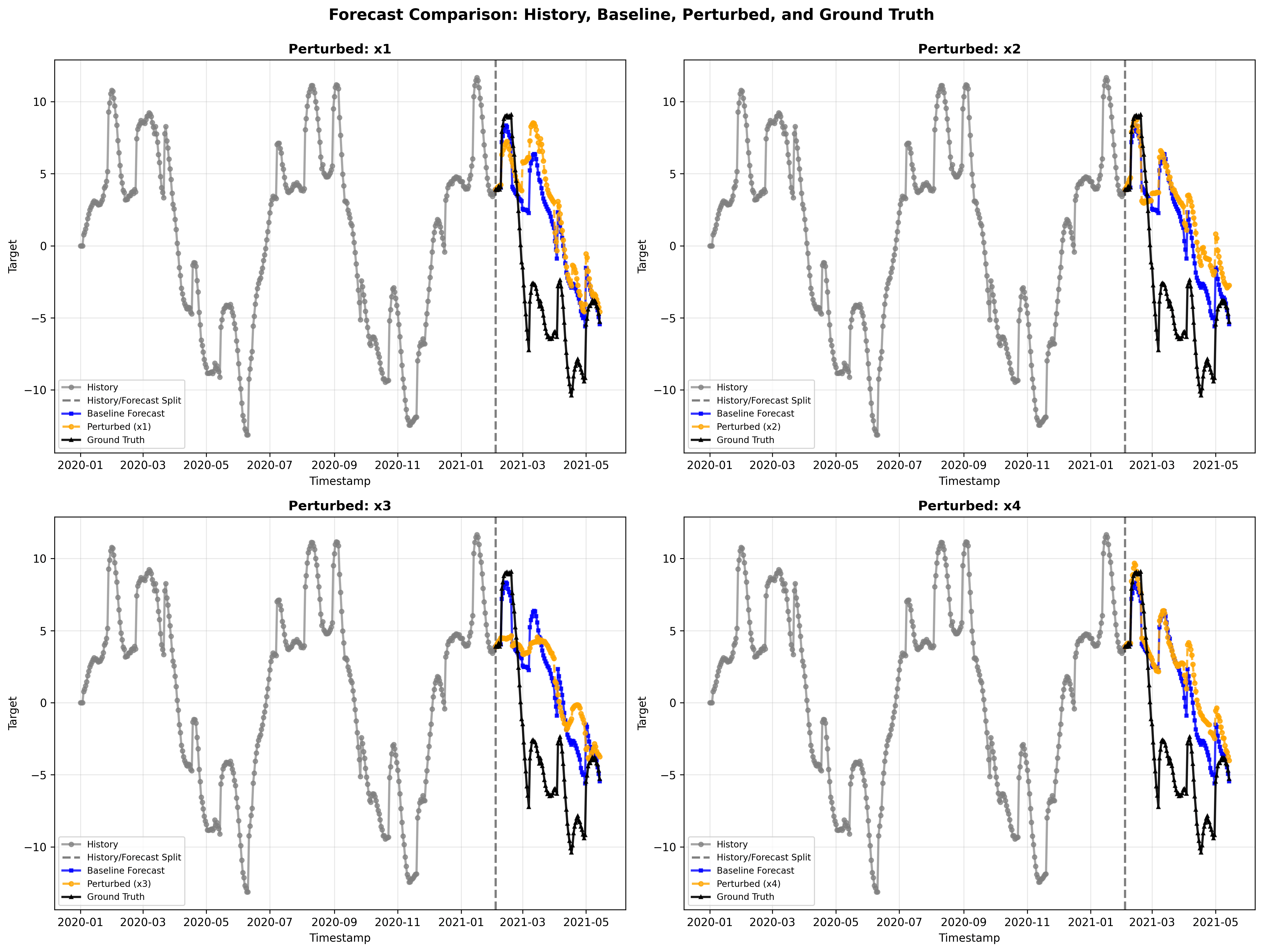
4.1 Forecast Comparison

We show the results of zero-perturbation for a randomly sampled ARX(3,4) time series. Each panel masks one covariate (x1–x4) using zero perturbation, replacing the covariate with a zero column (we only show the target time series):
  • Blue = baseline forecast
  • Orange = forecast with masked covariate
  • Larger divergence β‡’ stronger dependence on that covariate
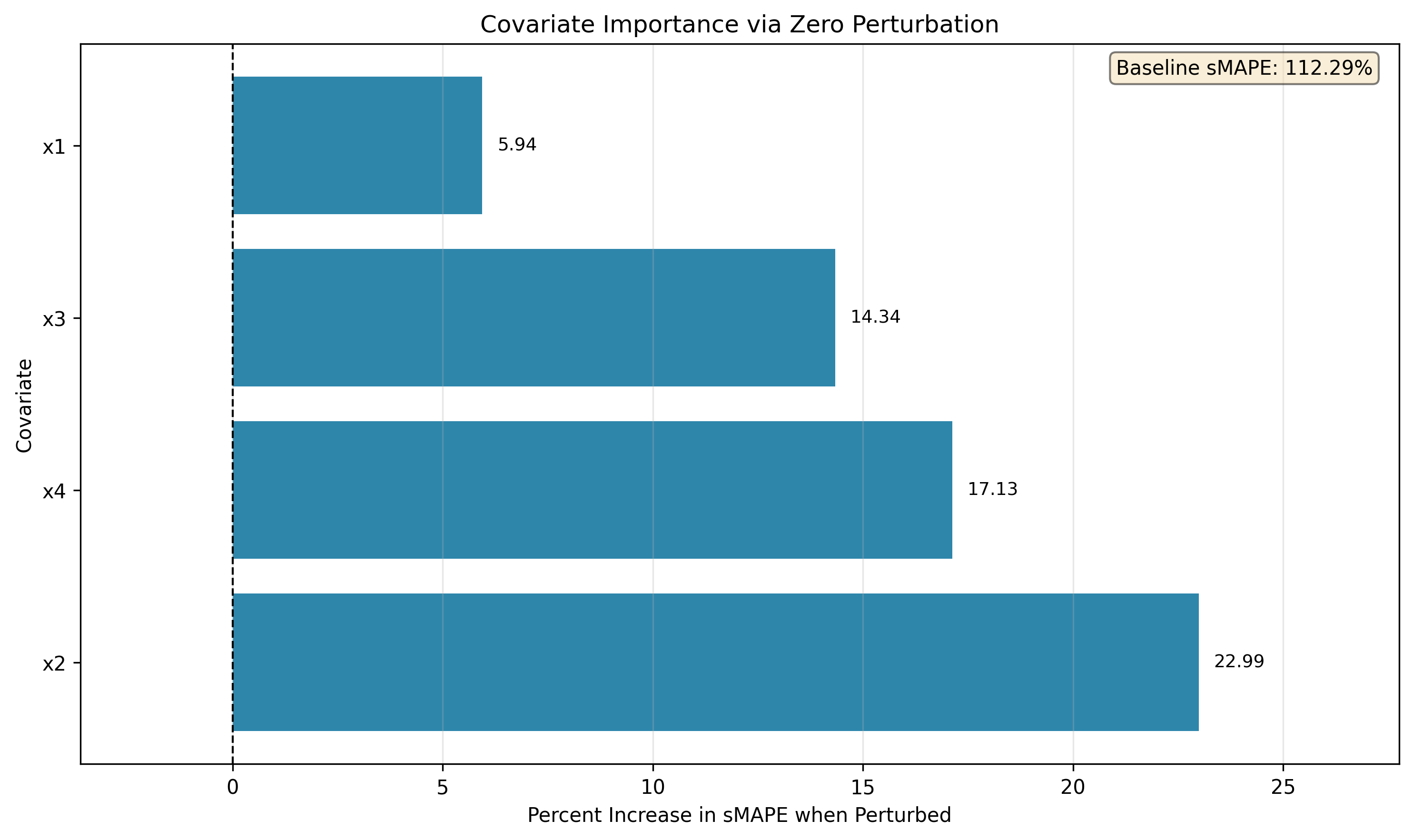
As we can see here, masking out some covariates can have significant effects on the overall prediction, while other changes are much more slight. For an individual run, the most impactful covariates may not be the ones with the highest coefficients, though we will see across runs that the results are consistent.

​
4.2 Per-Run Covariate Importance

CovariateΞ”-sMAPE (%)
x15.94
x222.99
x314.34
x417.13

​
🎲 5) Variability Across Seeds

Even though the ARX coefficients are kept constant, the exogenous signals are sampled randomly, producing variability across runs. We provide a sample from a different seed (resulting in different exogenous covariates) to indicate how this variability can affect the perturbation analysis on a per-run basis. This seed shows how variance can result in significantly different change in sMAPE from perturbation.

​
5.1 Forecast Comparison

​
5.2 Importance

CovariateΞ”-sMAPE (%)
x150.7
x24.0
x3-3.4
x40.3
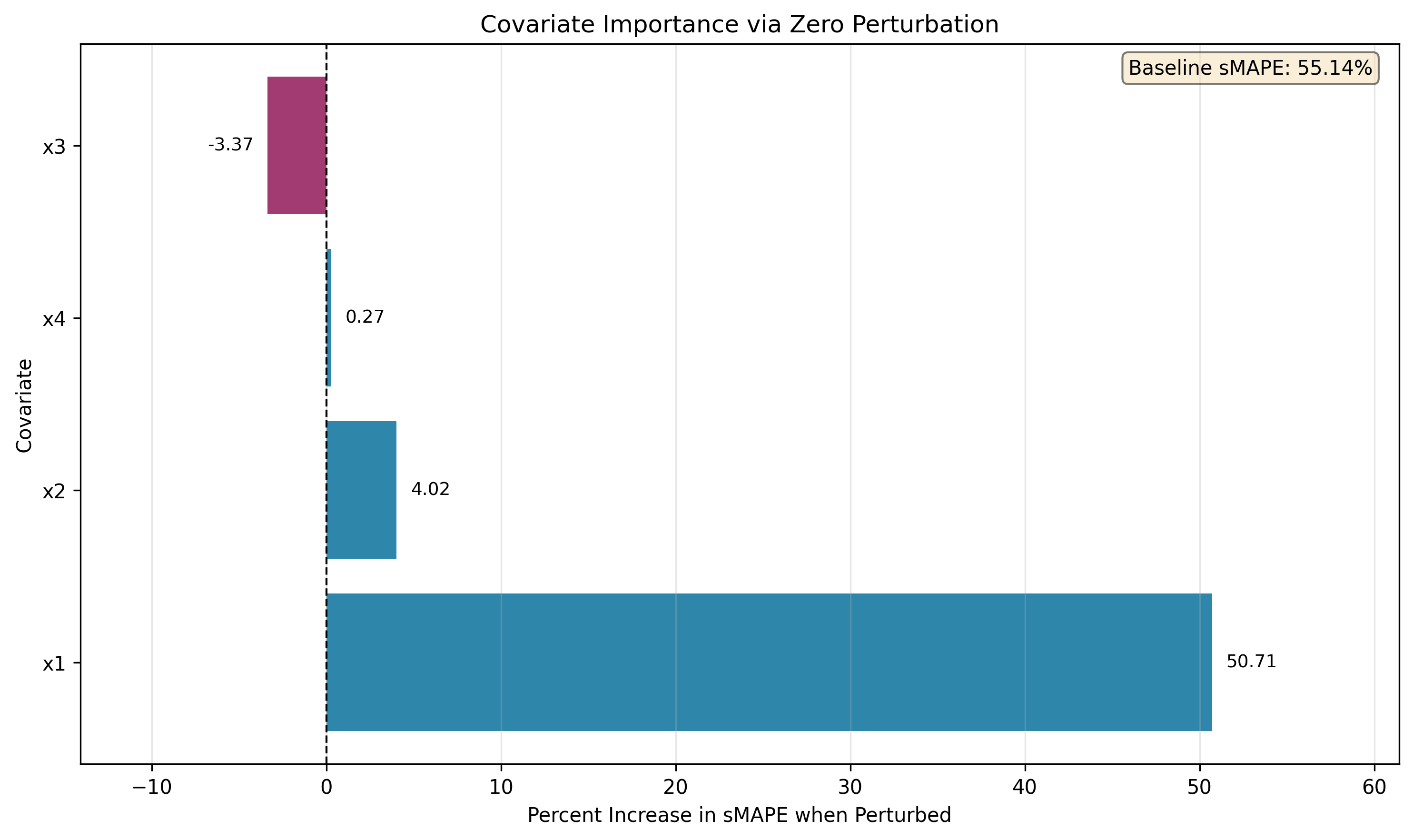
🧠 Single-run attribution is unreliable β€” use distributional analysis.

​
πŸ“ˆ 6) Aggregated Statistics Across 100 Samples

Even though individual runs may have variation in the perturbation analysis, the aggregated trends indicate that Zero-perturbation offers an efficient and meaningful indication of covariate importance. In this experiment, we generated 100 samples of ARX(3,4) data, with the same coefficients as indicated in Section 1.

​
6.1 Error-Shift Distributions

The error shift distribution indicates how often different relative sMAPE shift values occur across 100 samples. Notice that while skewed right (importance), there is quite a bit of variability and even negative (lower error after zero perturbation).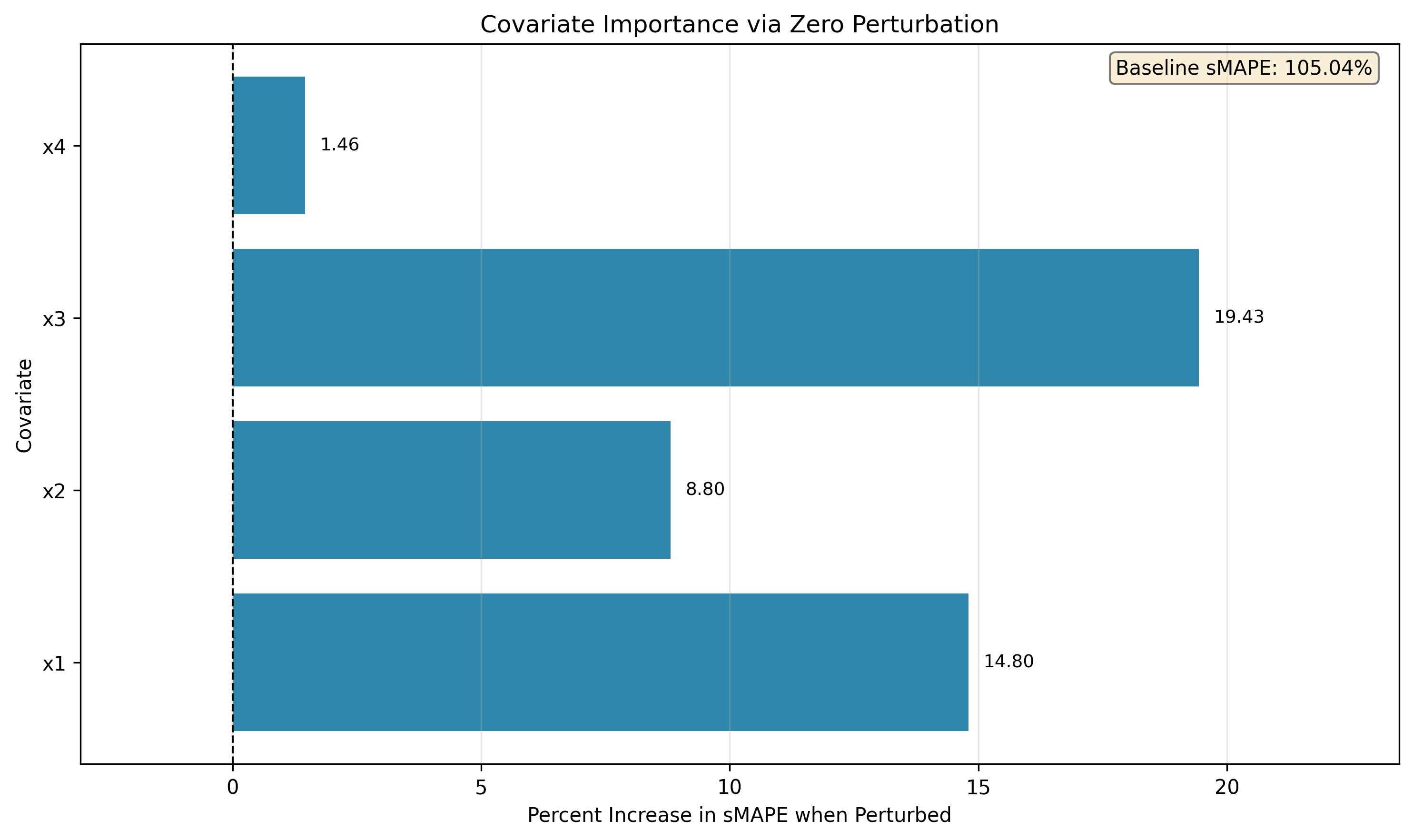

​
6.2 Mean Importance (Global Ranking)

Nonetheless, the aggregated importance is consistent with the weights of the ARX(3,4) data, indicating that zero perturbation is a good measure of covariate importance with sufficient data, correctly weighting the individual covariates according to their importance. 
| Covariate | Mean Ξ”-sMAPE | Interpretation            |
|-----------|---------------|---------------------------|
| x3        | 19.4%         | Strongest importance and high weight (0.9 coefficient in ARX equation)  |
| x1        | 14.8%         | Strong importance (0.8 coefficient in ARX)      |
| x2        | 8.8%          | Moderate importance (0.5 coefficient in ARX)      |
| x4        | 1.4%          | Weak importance (0.2 coefficient in ARX)   |

​
βœ… Key Takeaways

  • Zero-perturbation is a fast, retraining-free alternative to SHAP/LIME for time series. Note that because SHAP/LIME requires significantly more calls to the model, they can be too costly for substantial analysis.
  • Negative Importance can occur, indicative of unpredictability in the true forecast
  • Histograms reveal risk profiles: there can be variability in benefit across samples
  • ARX data allows us to pinpoint the current capabilities of the model.