Pricing Simulation

What is pricing simulation? How does it help?

Problem: Businesses struggle to find optimal pricing that maximizes revenue. Traditional methods rely on gut feeling, often leading to suboptimal pricing that either leaves money on the table or drives away customers. Our approach: We show how businesses can use Synthefy’s AI-powered forecasting to simulate different price points and automatically identify the optimal pricing strategy. Outcome: In this example, our models show a potential revenue increase of 9% by finding the optimal price point that balances demand and profitability.

1. Load Historical Sales Data

This dataset comes from a Fortune 500 company that sells a popular health product in a pharmacy. We’ll use their real sales and pricing history to uncover how data can drive smarter, more profitable pricing decisions.

import asyncio

import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import swarm_visualizer
from swarm_visualizer.utility import set_axis_infos
from swarm_visualizer.utility.general_utils import set_plot_properties
from synthefy.api_client import SynthefyAsyncAPIClient

# Set swarm-visualizer properties for consistent styling
set_plot_properties(usetex=False)

# Load the historical sales data
history_df = pd.read_csv(
    "https://drive.google.com/uc?export=download&id=1FtLW17XE1NHcV1bF8mLW_2WHVKzrHts_"
)
future_df = pd.read_csv(
    "https://drive.google.com/uc?export=download&id=1l2zG7GNTcdDm_HzKhhwii3GTI0Z99a9h"
)

Data Format: Your CSV should have columns like date, unit_price, and sales. The future_df represents the time periods you want to forecast for (without the sales column filled in yet).

2: Visualize Historical Data

Before running simulations, it’s important to understand your historical data. Let’s create visualizations to see how price and sales have changed over time, and whether there’s a correlation.

Show plotting code for historical analysis

def plot_historical_analysis(history_df):
    """
    Create two plots to analyze historical price and sales data using swarm-visualizer.

    Plot 1: Time series showing both unit price and sales over time (dual-axis)
    Plot 2: Correlation plot between unit price and sales

    Args:
        history_df: DataFrame with 'date', 'unit_price', and 'sales' columns
    """
    # Create figure with 2 rows and 1 column (vertical layout)
    fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(14, 10))

    # --- Plot 1: Historical Time Series Plot using swarm-visualizer ---
    # Prepare data for swarm-visualizer
    normalized_dict = {
        "Unit Price": {
            "x": history_df["date"],
            "y": history_df["unit_price"],
            "lw": 2.5,
            "linestyle": "--",
            "color": "black",  # Black dashed
            "alpha": 0.8,
            "zorder": 2,
        },
        "Sales": {
            "x": history_df["date"],
            "y": history_df["sales"],
            "lw": 2.5,
            "linestyle": "-",
            "color": "black",  # Black solid
            "alpha": 0.8,
            "zorder": 2,
        },
    }

    # Use swarm-visualizer plot_overlaid_lineplot
    swarm_visualizer.plot_overlaid_lineplot(
        ax=ax1,
        normalized_dict=normalized_dict,
        title_str="Historical Unit Price and Sales Over Time",
        ylabel="Unit Price / Sales",
        xlabel="Date",
        legend_present=True,
    )

    # Move legend to the right side outside the plot
    ax1.legend(loc="center left", bbox_to_anchor=(1, 0.5))

    # Use swarm-visualizer set_axis_infos for consistent styling
    set_axis_infos(
        ax=ax1,
        xlabel="Date",
        ylabel="Unit Price / Sales",
        title_str="Historical Unit Price and Sales Over Time",
        grid=True,
    )

    # Format x-axis labels - reduce label frequency and font size
    ax1.set_xticks(ax1.get_xticks()[::2])
    plt.setp(ax1.get_xticklabels(), rotation=45, ha="right", fontsize=12)

    # --- Plot 2: Correlation Plot ---
    corr_val = (
        history_df[["unit_price", "sales"]].corr().loc["unit_price", "sales"]
    )

    sns.regplot(
        x="unit_price",
        y="sales",
        data=history_df,
        marker="o",
        color="black",  # Black points
        line_kws={"color": "#E63946", "lw": 2, "label": f"Corr={corr_val:.2f}"},
        ax=ax2,
        scatter_kws={"alpha": 1.0},
        ci=None,
    )
    ax2.set_xlabel("Unit Price ($)", fontsize=12)
    ax2.set_ylabel("Sales", fontsize=12)
    ax2.set_title(
        "Correlation Between Unit Price and Sales",
        fontsize=13,
        weight="semibold",
    )
    ax2.legend()
    ax2.grid(True, linestyle="--", alpha=0.4)

    plt.tight_layout()
    plt.savefig("pricing_data_visualization.png", dpi=300, bbox_inches="tight")
    plt.show()



# Visualize the historical data
plot_historical_analysis(history_df)

The time series plot shows trends over time, while the correlation plot reveals if there’s a linear relationship between price and demand. A negative correlation suggests demand decreases as price increases (price sensitivity).

Example Output: Historical Data Analysis

The visualizations above show:

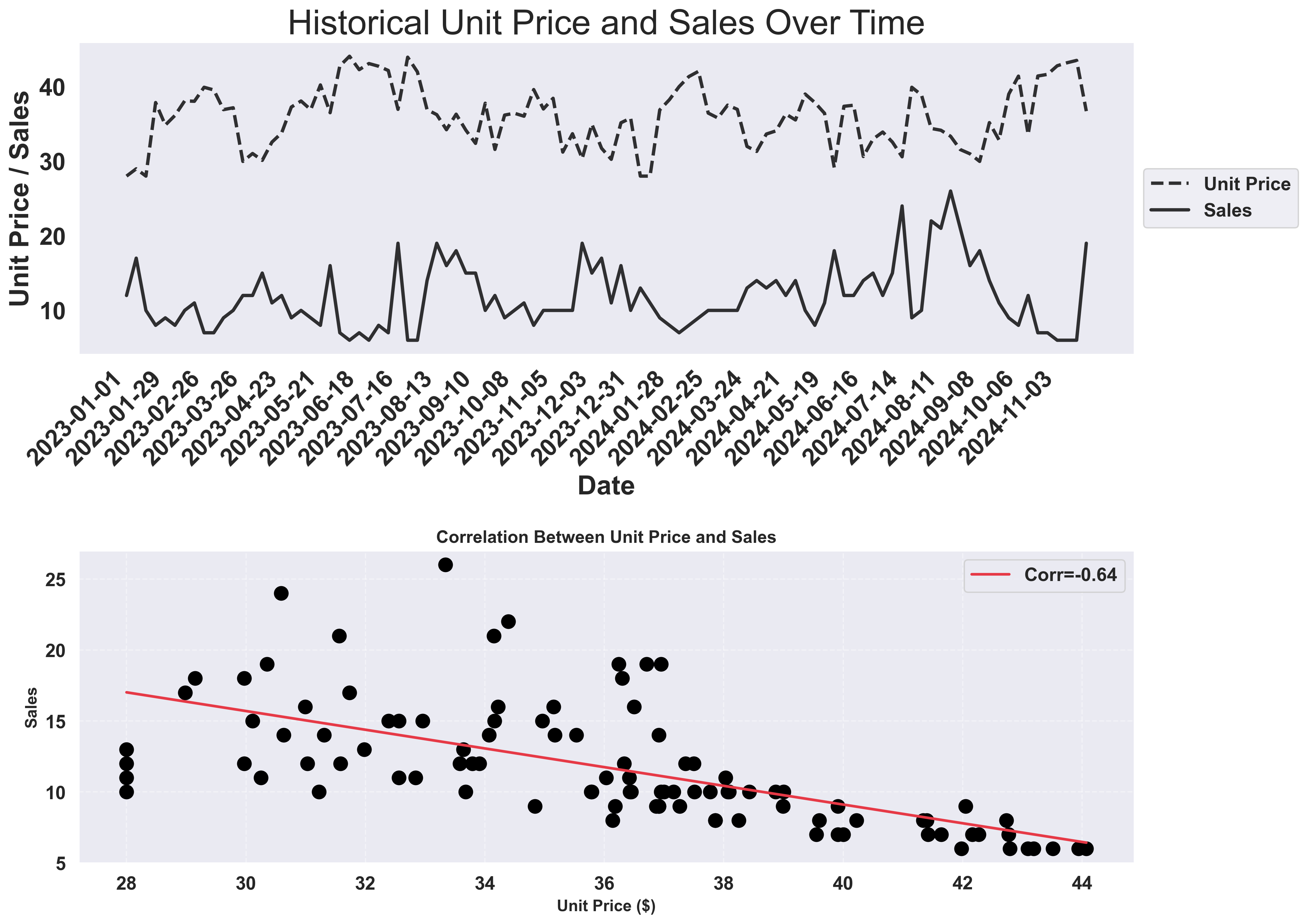
Top panels: How unit price and sales volume have varied over 2 years of weekly data
Bottom panel: A clear negative correlation (-0.64) between price and sales, confirming price sensitivity

Step 3: Set Up Pricing Simulation

Now, let’s define the range of prices we want to test. We’ll create a range of 11 price points ranging from 85% to 115% of your historical average price. We’ll call this the “base” price, and use it as a basline for comparison.

# Calculate base price from historical data
base_price = history_df["unit_price"].mean()

# Create price range (11 price points from 85% to 115% of base price)
price_simulation_range = np.linspace(base_price * 0.85, base_price * 1.15, 11)

print(f"Testing prices from ${price_simulation_range[0]:.2f} to ${price_simulation_range[-1]:.2f}")

Adjust the range: You can modify the 0.85 and 1.15 multipliers to test a wider or narrower price range. For example, use 0.7 and 1.3 to test 70% to 130% of the base price.

Step 4: Prepare Data for Forecasting

For each price point, we need to create a separate forecast scenario. We’ll duplicate the future DataFrame and modify the unit_price column for each scenario.

# Data preparation for pricing simulation
target_dfs = []
for price in price_simulation_range:
    modified_future = future_df.copy()
    modified_future["unit_price"] = price
    target_dfs.append(modified_future)

Step 5: Run AI Forecasts

async def get_forecasts():
    async with SynthefyAsyncAPIClient() as api_client:
        results = await api_client.forecast_dfs(
            history_dfs=[history_df] * len(price_simulation_range),
            target_dfs=target_dfs,
            target_col="sales",
            timestamp_col="date",
            metadata_cols=["unit_price"],
            leak_cols=["unit_price"],
            model="Migas-1.0",
        )
        return results


# Run the async forecast function
results = asyncio.run(get_forecasts())
print(f"✓ Received {len(results)} forecast results")

Key parameters:

metadata_cols=["unit_price"]: Features the model can use
leak_cols=["unit_price"]: Features that are known in advance (price is controllable)

Step 6: Create Time Series Forecast Visualization

First, let’s create a comprehensive time series visualization that shows all forecast scenarios overlaid on the historical data.

Show time series visualization code

def plot_forecast_time_series(
    history_df,
    future_df,
    results,
    price_simulation_range,
    base_price,
    optimal_price,
):
    """
    Plot historical data and all forecasts for different prices using swarm-visualizer.

    This function creates a comprehensive visualization showing:
    - Historical sales data (black line)
    - Multiple forecast scenarios for different prices (orange gradient)
    - Highlighted optimal and base price forecasts
    - Forecast region background highlighting

    Args:
        history_df: DataFrame with historical sales data
        future_df: DataFrame with future dates for forecasting
        results: List of forecast results for each price point
        price_simulation_range: Array of price points tested
        base_price: Current/average price from historical data
        optimal_price: Price that maximizes revenue
    """
    # Create figure with consistent sizing following hotel demand pattern
    fig, ax = plt.subplots(figsize=(20, 6))

    # Get future dates
    future_dates = future_df["date"].tolist()

    # Prepare data for swarm-visualizer - show only last 50% of history
    history_cutoff = len(history_df) // 2
    history_subset = history_df.iloc[history_cutoff:]

    # Prepare normalized dictionary for swarm-visualizer
    normalized_dict = {
        "Historical Sales": {
            "x": history_subset["date"],
            "y": history_subset["sales"],
            "lw": 3,
            "linestyle": "-",
            "color": "black",
            "alpha": 0.8,
            "zorder": 5,
        }
    }

    # Create orange gradient colors for all price points
    orange_colors = cm.Oranges(
        np.linspace(0.3, 0.9, len(price_simulation_range))
    )

    # Plot ALL forecasts - every single price point!
    for i, (price, result) in enumerate(zip(price_simulation_range, results)):
        forecast_values = result["sales"].tolist()

        # Combine historical data with forecast for this price
        historical_dates = history_subset["date"].tolist()
        historical_sales = history_subset["sales"].tolist()

        # Combine historical + forecast dates and values
        combined_dates = historical_dates + future_dates
        combined_sales = historical_sales + forecast_values

        # Determine styling based on price type - all using orange gradient
        color = orange_colors[i]  # Each price gets its own orange shade

        if abs(price - optimal_price) < 0.01:
            label = f"Optimal Price (${price:.2f})"
            linewidth = 4
            alpha = 1.0
        elif abs(price - base_price) < 0.01:
            label = f"Base Price (${price:.2f})"
            linewidth = 4
            alpha = 1.0
        else:
            label = f"${price:.2f}"
            linewidth = 2.0
            alpha = 0.8

        normalized_dict[label] = {
            "x": combined_dates,
            "y": combined_sales,
            "lw": linewidth,
            "linestyle": "-",
            "color": color,
            "alpha": alpha,
            "zorder": 4,
        }

    # Use swarm-visualizer plot_overlaid_lineplot
    swarm_visualizer.plot_overlaid_lineplot(
        ax=ax,
        normalized_dict=normalized_dict,
        title_str="Pricing Simulation: Complete Time Series with Forecasts by Price",
        ylabel="Sales",
        xlabel="Date",
        legend_present=True,
    )

    # Move legend to the right side outside the plot (following inventory_forecasting_demo.py pattern)
    ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))

    # Add vertical line to separate historical from forecast (following hotel_demand.py pattern)
    last_historical_date = history_subset["date"].iloc[-1]
    ax.axvline(
        x=last_historical_date,
        color="red",
        linestyle="--",
        linewidth=2,
        alpha=0.7,
        label="Train/Test Split",
        zorder=1,
    )

    # Use swarm-visualizer set_axis_infos for consistent styling
    set_axis_infos(
        ax=ax,
        xlabel="Date",
        ylabel="Sales",
        title_str="Pricing Simulation: Forecasts for Different Prices",
        grid=True,
    )

    # Format x-axis labels following hotel demand pattern - reduce label frequency
    # Only show every other tick to reduce clutter
    ax.set_xticks(ax.get_xticks()[::2])
    plt.xticks(rotation=45, ha="right")

    plt.tight_layout()
    plt.savefig("forecast_time_series.png", dpi=300, bbox_inches="tight")
    plt.show()

# Create time series visualization showing all forecasts
print("📊 Creating time series visualization of all forecasts...")
plot_forecast_time_series(
    history_df,
    future_df,
    results,
    price_simulation_range,
    base_price,
    optimal_price,
)

Example Output: Time Series Forecast Visualization

This comprehensive visualization shows:

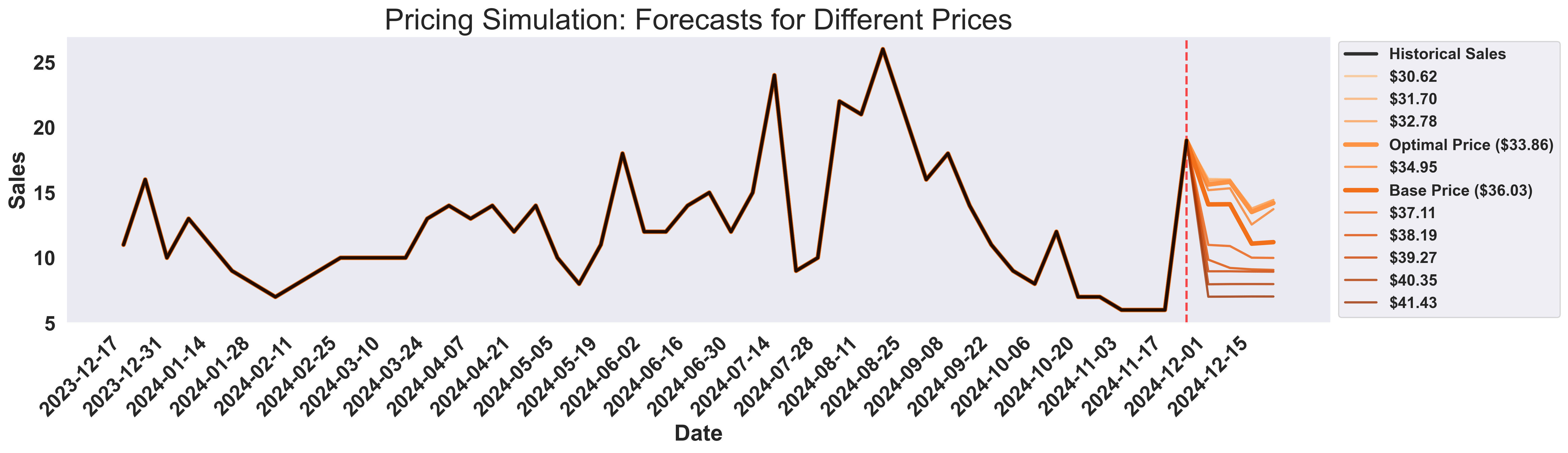
Black line: Historical sales data (last 50% for focus)
Orange gradient lines: All forecast scenarios for different prices
Light blue background: Highlights the forecast region
Optimal & Base prices: Thicker lines for key scenarios

Step 7: Analyze Results

Extract the forecasts and calculate revenue for each price point. Then identify the optimal price that maximizes revenue.

# Extract forecasts (mean sales for each price point)
forecasts = [int(round(result["sales"].mean())) for result in results]

# Calculate revenue for each price point
revenues = [price * forecast for price, forecast in zip(price_simulation_range, forecasts)]

# Find optimal price point
optimal_idx = np.argmax(revenues)
optimal_price = price_simulation_range[optimal_idx]
optimal_transactions = forecasts[optimal_idx]
optimal_revenue = revenues[optimal_idx]

# Find base price index (closest to current average price)
base_idx = np.argmin(np.abs(price_simulation_range - base_price))
base_transactions = forecasts[base_idx]
base_revenue = revenues[base_idx]

Step 8: Visualize Pricing Insights

Finally, let’s create comprehensive visualizations to understand the price-demand relationship and identify the optimal pricing strategy.

Show visualization code

# Create 3-plot visualization
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 5))
fig.suptitle(
    "Pricing Simulation Analysis", fontsize=18, fontweight="bold", y=0.95
)

# Plot 1: Price vs Sales (Partial Dependence Plot)
fig1, ax1 = plt.subplots(figsize=(10, 6))

# Prepare data for swarm-visualizer
normalized_dict = {
    "Forecasted Sales": {
        "x": price_simulation_range,
        "y": forecasts,
        "lw": 2.5,
        "linestyle": "--",
        "color": "#fea333",  # Orange
        "alpha": 0.9,
        "zorder": 3,
    },
    "Base Price": {
        "x": [base_price, base_price],
        "y": [min(forecasts), max(forecasts)],
        "lw": 2,
        "linestyle": "--",
        "color": "black",
        "alpha": 0.8,
        "zorder": 2,
    },
}

# Use swarm-visualizer plot_overlaid_lineplot
swarm_visualizer.plot_overlaid_lineplot(
    ax=ax1,
    normalized_dict=normalized_dict,
    title_str="Partial Dependence Plot (Price vs Avg Forecasted Sales)",
    ylabel="Avg Forecasted Sales",
    xlabel="Sales Price ($)",
    legend_present=True,
)

# Use swarm-visualizer set_axis_infos for consistent styling
set_axis_infos(
    ax=ax1,
    xlabel="Sales Price ($)",
    ylabel="Avg Forecasted Sales",
    title_str="Partial Dependence Plot (Price vs Avg Forecasted Sales)",
    grid=True,
)

plt.tight_layout()
plt.savefig("price_vs_sales.png", dpi=300, bbox_inches="tight")
plt.show()

# Plot 2: Price vs Revenue
fig2, ax2 = plt.subplots(figsize=(10, 6))

# Prepare data for swarm-visualizer
normalized_dict = {
    "Expected Revenue": {
        "x": price_simulation_range,
        "y": revenues,
        "lw": 2.5,
        "linestyle": "--",
        "color": "#fea333",  # Orange
        "alpha": 0.9,
        "zorder": 3,
    },
    "Base Price": {
        "x": [base_price, base_price],
        "y": [min(revenues), max(revenues)],
        "lw": 2,
        "linestyle": "--",
        "color": "black",
        "alpha": 0.8,
        "zorder": 2,
    },
    "Optimal Price": {
        "x": [optimal_price, optimal_price],
        "y": [min(revenues), max(revenues)],
        "lw": 2,
        "linestyle": "--",
        "color": "#2ECC71",
        "alpha": 0.8,
        "zorder": 2,
    },
    "Optimal Point": {
        "x": [optimal_price],
        "y": [optimal_revenue],
        "lw": 0,
        "linestyle": "",
        "color": "#2ECC71",
        "alpha": 1.0,
        "zorder": 5,
        "marker": "o",
        "markersize": 6,
    },
}

# Use swarm-visualizer plot_overlaid_lineplot
swarm_visualizer.plot_overlaid_lineplot(
    ax=ax2,
    normalized_dict=normalized_dict,
    title_str="Price vs Revenue Optimization",
    ylabel="Expected Revenue ($)",
    xlabel="Sales Price ($)",
    legend_present=True,
)

# Use swarm-visualizer set_axis_infos for consistent styling
set_axis_infos(
    ax=ax2,
    xlabel="Sales Price ($)",
    ylabel="Expected Revenue ($)",
    title_str="Price vs Revenue Optimization",
    grid=True,
)

# Format y-axis for revenue
ax2.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, p: f"${x:,.0f}"))

plt.tight_layout()
plt.savefig("price_vs_revenue.png", dpi=300, bbox_inches="tight")
plt.show()

# Plot 3: Revenue comparison bar chart
fig3, ax3 = plt.subplots(figsize=(8, 6))

# Create bar chart with consistent styling
bar_colors = ["black", "#51CF66"]
bars = ax3.bar(
    [
        "Base Price\n" + f"${base_price:.2f}",
        "Optimal Price\n" + f"${optimal_price:.2f}",
    ],
    [base_revenue, optimal_revenue],
    color=bar_colors,
    alpha=0.8,
    edgecolor="black",
    linewidth=2,
)

# Use swarm-visualizer set_axis_infos for consistent styling
set_axis_infos(
    ax=ax3,
    xlabel="Pricing Strategy",
    ylabel="Expected Revenue ($)",
    title_str="Revenue Comparison",
    grid=True,
)

# Add value labels on bars
for bar in bars:
    height = bar.get_height()
    ax3.text(
        bar.get_x() + bar.get_width() / 2.0,
        height,
        f"${height:,.0f}",
        ha="center",
        va="bottom",
        fontsize=11,
        fontweight="bold",
    )

# Format y-axis for revenue
ax3.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, p: f"${x:,.0f}"))

plt.tight_layout()
plt.savefig("revenue_comparison.png", dpi=300, bbox_inches="tight")
plt.show()

Example Output: Pricing Simulation Results

Plot 1: Price vs Sales Analysis

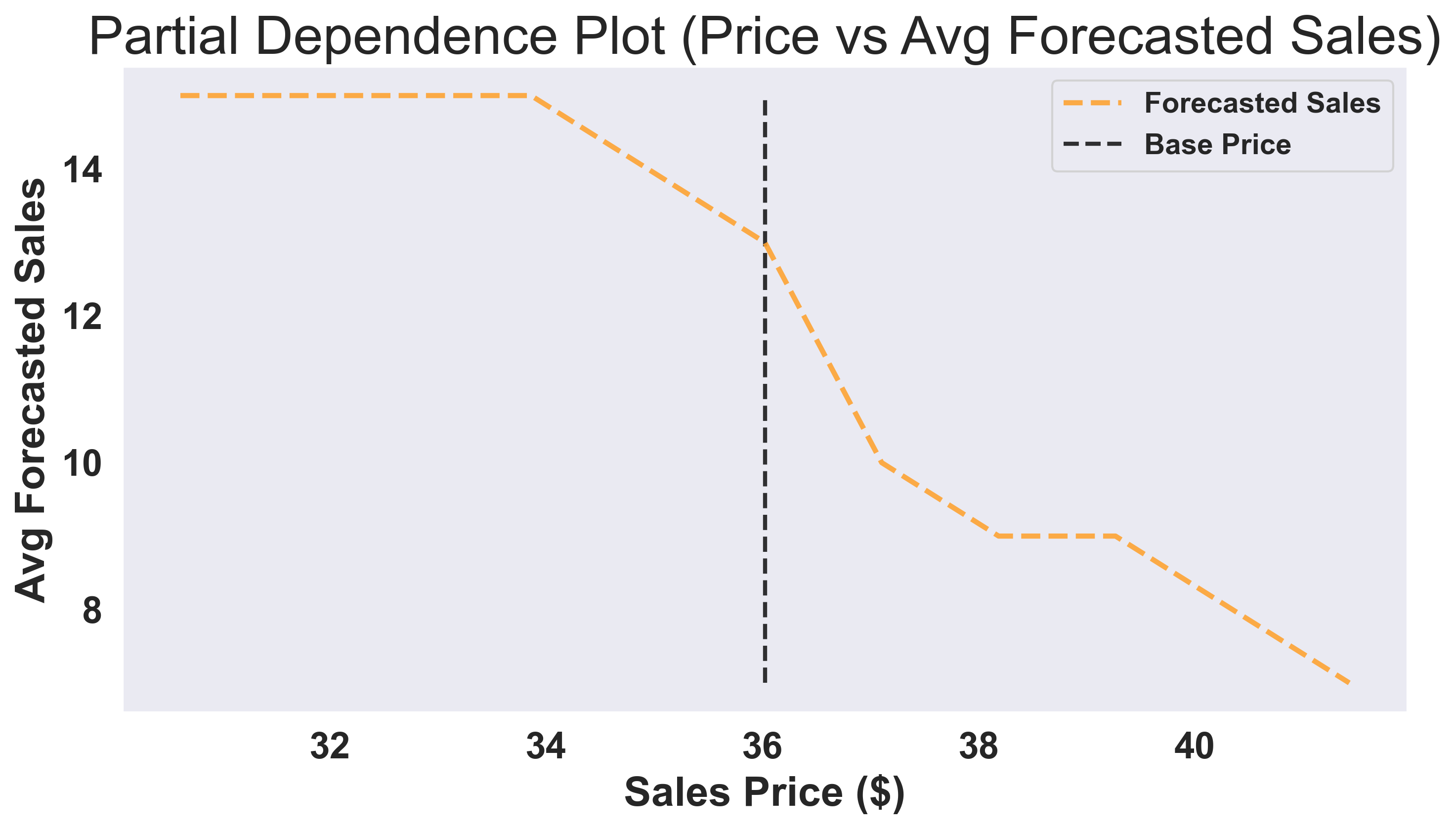
Plot 2: Price vs Revenue Optimization

Plot 3: Revenue Comparison

Now you can answer critical business questions:

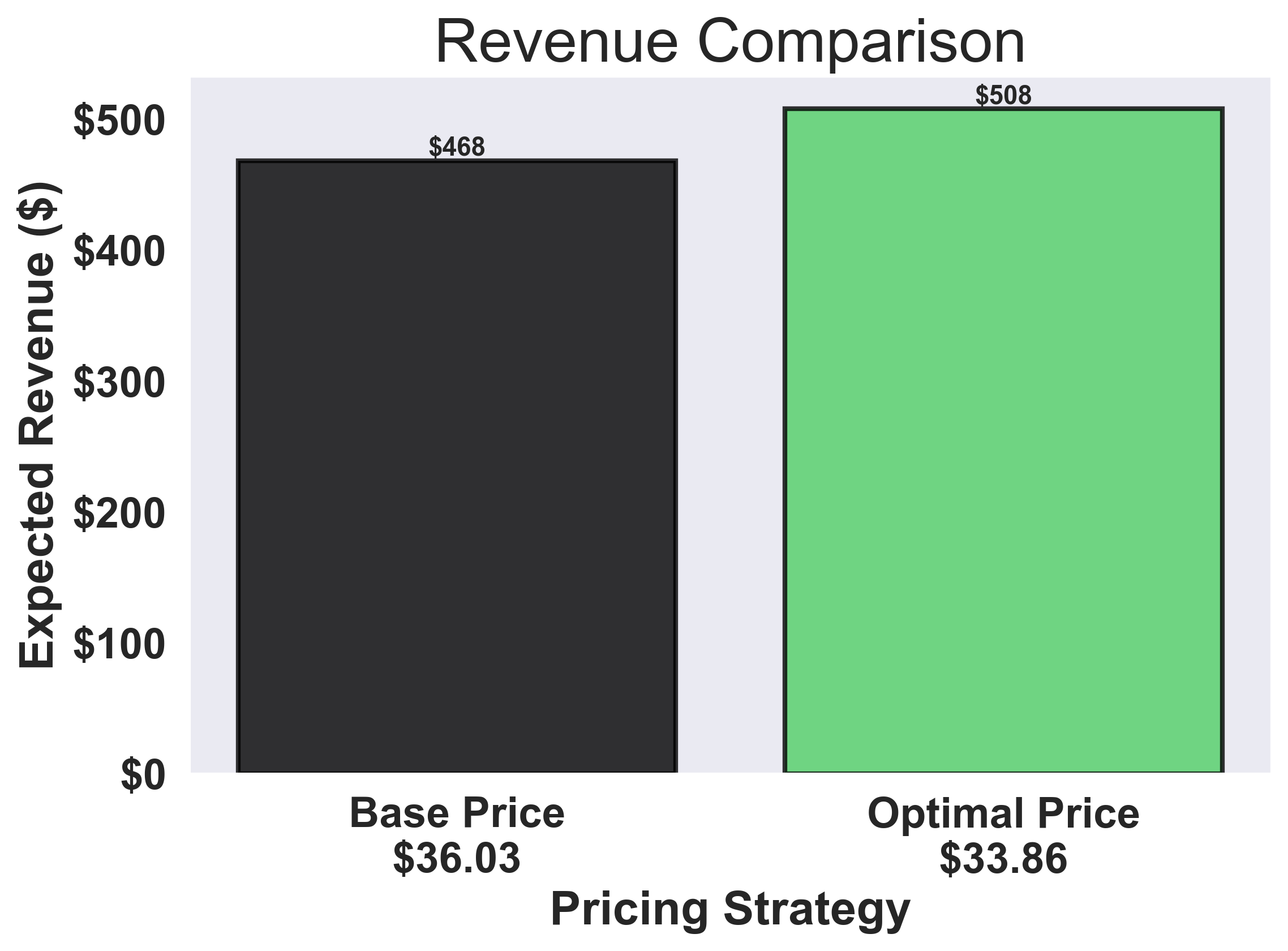
How price-sensitive are my customers? → Look at Plot 1 (steeper slope = more sensitivity)
What’s my optimal price? → Look at Plot 2 (green marker)
How much revenue am I leaving on the table? → Look at Plot 3 (red vs green bars)

Complete Code

Here’s the full working example you can run:

Show complete code

import asyncio

import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import swarm_visualizer
from swarm_visualizer.utility import set_axis_infos
from swarm_visualizer.utility.general_utils import set_plot_properties
from synthefy.api_client import SynthefyAsyncAPIClient

# Set swarm-visualizer properties for consistent styling
set_plot_properties(usetex=False)

# Step 1: Load Your Historical Sales Data
history_df = pd.read_csv(
    "https://drive.google.com/uc?export=download&id=1FtLW17XE1NHcV1bF8mLW_2WHVKzrHts_"
)
future_df = pd.read_csv(
    "https://drive.google.com/uc?export=download&id=1l2zG7GNTcdDm_HzKhhwii3GTI0Z99a9h"
)


def plot_historical_analysis(history_df):
    """
    Create two plots to analyze historical price and sales data using swarm-visualizer.

    Plot 1: Time series showing both unit price and sales over time (dual-axis)
    Plot 2: Correlation plot between unit price and sales

    Args:
        history_df: DataFrame with 'date', 'unit_price', and 'sales' columns
    """
    # Create figure with 2 rows and 1 column (vertical layout)
    fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(14, 10))

    # --- Plot 1: Historical Time Series Plot using swarm-visualizer ---
    # Prepare data for swarm-visualizer
    normalized_dict = {
        "Unit Price": {
            "x": history_df["date"],
            "y": history_df["unit_price"],
            "lw": 2.5,
            "linestyle": "--",
            "color": "black",  # Black dashed
            "alpha": 0.8,
            "zorder": 2,
        },
        "Sales": {
            "x": history_df["date"],
            "y": history_df["sales"],
            "lw": 2.5,
            "linestyle": "-",
            "color": "black",  # Black solid
            "alpha": 0.8,
            "zorder": 2,
        },
    }

    # Use swarm-visualizer plot_overlaid_lineplot
    swarm_visualizer.plot_overlaid_lineplot(
        ax=ax1,
        normalized_dict=normalized_dict,
        title_str="Historical Unit Price and Sales Over Time",
        ylabel="Unit Price / Sales",
        xlabel="Date",
        legend_present=True,
    )

    # Move legend to the right side outside the plot
    ax1.legend(loc="center left", bbox_to_anchor=(1, 0.5))

    # Use swarm-visualizer set_axis_infos for consistent styling
    set_axis_infos(
        ax=ax1,
        xlabel="Date",
        ylabel="Unit Price / Sales",
        title_str="Historical Unit Price and Sales Over Time",
        grid=True,
    )

    # Format x-axis labels - reduce label frequency and font size
    ax1.set_xticks(ax1.get_xticks()[::2])
    plt.setp(ax1.get_xticklabels(), rotation=45, ha="right", fontsize=12)

    # --- Plot 2: Correlation Plot ---
    corr_val = (
        history_df[["unit_price", "sales"]].corr().loc["unit_price", "sales"]
    )

    sns.regplot(
        x="unit_price",
        y="sales",
        data=history_df,
        marker="o",
        color="black",  # Black points
        line_kws={"color": "#E63946", "lw": 2, "label": f"Corr={corr_val:.2f}"},
        ax=ax2,
        scatter_kws={"alpha": 1.0},
        ci=None,
    )
    ax2.set_xlabel("Unit Price ($)", fontsize=12)
    ax2.set_ylabel("Sales", fontsize=12)
    ax2.set_title(
        "Correlation Between Unit Price and Sales",
        fontsize=13,
        weight="semibold",
    )
    ax2.legend()
    ax2.grid(True, linestyle="--", alpha=0.4)

    plt.tight_layout()
    plt.savefig("pricing_data_visualization.png", dpi=300, bbox_inches="tight")
    plt.show()


# Step 2: Visualize Historical Data
plot_historical_analysis(history_df)

# Step 3: Set Up Price Grid
base_price = history_df["unit_price"].mean()
price_simulation_range = np.linspace(base_price * 0.85, base_price * 1.15, 11)
print(f"Testing prices from ${price_simulation_range[0]:.2f} to ${price_simulation_range[-1]:.2f}")

# Step 4: Prepare Data for Forecasting
target_dfs = []
for price in price_simulation_range:
    modified_future = future_df.copy()
    modified_future["unit_price"] = price
    target_dfs.append(modified_future)


# Step 5: Run AI Forecasts
async def get_forecasts():
    async with SynthefyAsyncAPIClient() as api_client:
        results = await api_client.forecast_dfs(
            history_dfs=[history_df] * len(price_simulation_range),
            target_dfs=target_dfs,
            target_col="sales",
            timestamp_col="date",
            metadata_cols=["unit_price"],
            leak_cols=["unit_price"],
            model="Migas-1.0",
        )
        return results


results = asyncio.run(get_forecasts())
print(f"✓ Received {len(results)} forecast results")

# Step 6: Analyze Results
forecasts = [int(round(result["sales"].mean())) for result in results]
revenues = [price * forecast for price, forecast in zip(price_simulation_range, forecasts)]

optimal_idx = np.argmax(revenues)
optimal_price = price_simulation_range[optimal_idx]
optimal_revenue = revenues[optimal_idx]

base_idx = np.argmin(np.abs(price_simulation_range - base_price))
base_revenue = revenues[base_idx]

# Step 6: Create Time Series Forecast Visualization
def plot_forecast_time_series(
    history_df,
    future_df,
    results,
    price_simulation_range,
    base_price,
    optimal_price,
):
    """Plot historical data and all forecasts for different prices using swarm-visualizer."""
    fig, ax = plt.subplots(figsize=(20, 6))

    # Get future dates
    future_dates = future_df["date"].tolist()

    # Prepare data for swarm-visualizer - show only last 50% of history
    history_cutoff = len(history_df) // 2
    history_subset = history_df.iloc[history_cutoff:]

    normalized_dict = {
        "Historical Sales": {
            "x": history_subset["date"],
            "y": history_subset["sales"],
            "lw": 3,
            "linestyle": "-",
            "color": "black",
            "alpha": 0.8,
            "zorder": 5,
        }
    }

    # Plot ALL forecasts - every single price point!
    # Orange gradient color scheme for all forecasts
    # Create orange gradient colors for all price points
    orange_colors = cm.Oranges(
        np.linspace(0.3, 0.9, len(price_simulation_range))
    )

    for i, (price, result) in enumerate(zip(price_simulation_range, results)):
        forecast_values = result["sales"].tolist()

        # Combine historical data with forecast for this price
        # Historical data (same for all prices) - only last 50%
        historical_dates = history_subset["date"].tolist()
        historical_sales = history_subset["sales"].tolist()

        # Combine historical + forecast dates and values
        combined_dates = historical_dates + future_dates
        combined_sales = historical_sales + forecast_values

        # Determine styling based on price type - all using orange gradient
        color = orange_colors[i]  # Each price gets its own orange shade

        if abs(price - optimal_price) < 0.01:
            label = f"Optimal Price (${price:.2f})"
            linewidth = 4
            alpha = 1.0
        elif abs(price - base_price) < 0.01:
            label = f"Base Price (${price:.2f})"
            linewidth = 4
            alpha = 1.0
        else:
            label = f"${price:.2f}"
            linewidth = 2.0
            alpha = 0.8

        normalized_dict[label] = {
            "x": combined_dates,
            "y": combined_sales,
            "lw": linewidth,
            "linestyle": "-",
            "color": color,
            "alpha": alpha,
            "zorder": 4,
        }

    # Use swarm-visualizer plot_overlaid_lineplot
    swarm_visualizer.plot_overlaid_lineplot(
        ax=ax,
        normalized_dict=normalized_dict,
        title_str="Pricing Simulation: Complete Time Series with Forecasts by Price",
        ylabel="Sales",
        xlabel="Date",
        legend_present=True,
    )

    # Add light blue background for the forecast region
    last_historical_date = history_subset["date"].iloc[-1]
    last_forecast_date = future_df["date"].iloc[-1]

    # Add light blue background for the forecast region
    ax.axvspan(
        xmin=last_historical_date,
        xmax=last_forecast_date,
        ymin=0,
        ymax=1,
        color="lightblue",
        alpha=0.2,
        zorder=1,
        label="Forecast Region",
    )

    # Add light blue vertical line to separate historical from forecast
    ax.axvline(
        x=last_historical_date,
        color="lightblue",
        linestyle="-",
        alpha=0.8,
        linewidth=3,
        zorder=3,
    )
    ax.text(
        last_historical_date,
        ax.get_ylim()[1] * 0.95,
        "Forecasts",
        ha="left",
        va="top",
        fontsize=12,
        color="black",
        weight="bold",
        zorder=6,
    )

    # Use swarm-visualizer set_axis_infos for consistent styling
    set_axis_infos(
        ax=ax,
        xlabel="Date",
        ylabel="Sales",
        title_str="Simulation: Forecasts for Different Prices",
        grid=True,
    )
    # Rotate x-axis labels to prevent overlap and improve readability
    plt.setp(ax.get_xticklabels(), rotation=45, ha="right", fontsize=10)

    plt.savefig("forecast_time_series.png", dpi=300, bbox_inches="tight")
    plt.show()

# Create time series visualization showing all forecasts
print("📊 Creating time series visualization of all forecasts...")
plot_forecast_time_series(
    history_df,
    future_df,
    results,
    price_simulation_range,
    base_price,
    optimal_price,
)

# Step 7: Analyze Results
forecasts = [int(round(result["sales"].mean())) for result in results]
revenues = [price * forecast for price, forecast in zip(price_simulation_range, forecasts)]

optimal_idx = np.argmax(revenues)
optimal_price = price_simulation_range[optimal_idx]
optimal_revenue = revenues[optimal_idx]

base_idx = np.argmin(np.abs(price_simulation_range - base_price))
base_revenue = revenues[base_idx]

# Step 8: Visualize Pricing Insights - Create separate plots for each analysis

# Plot 1: Price vs Sales (Partial Dependence Plot)
print("📊 Creating Price vs Sales plot...")
fig1, ax1 = plt.subplots(figsize=(10, 6))

# Prepare data for swarm-visualizer
normalized_dict = {
    "Forecasted Sales": {
        "x": price_simulation_range,
        "y": forecasts,
        "lw": 2.5,
        "linestyle": "--",
        "color": "#fea333",  # Orange
        "alpha": 0.9,
        "zorder": 3,
    },
    "Base Price": {
        "x": [base_price, base_price],
        "y": [min(forecasts), max(forecasts)],
        "lw": 2,
        "linestyle": "--",
        "color": "black",
        "alpha": 0.8,
        "zorder": 2,
    },
}

# Use swarm-visualizer plot_overlaid_lineplot
swarm_visualizer.plot_overlaid_lineplot(
    ax=ax1,
    normalized_dict=normalized_dict,
    title_str="Partial Dependence Plot (Price vs Avg Forecasted Sales)",
    ylabel="Avg Forecasted Sales",
    xlabel="Sales Price ($)",
    legend_present=True,
)

# Use swarm-visualizer set_axis_infos for consistent styling
set_axis_infos(
    ax=ax1,
    xlabel="Sales Price ($)",
    ylabel="Avg Forecasted Sales",
    title_str="Partial Dependence Plot (Price vs Avg Forecasted Sales)",
    grid=True,
)

plt.tight_layout()
plt.savefig("price_vs_sales.png", dpi=300, bbox_inches="tight")
plt.show()

# Plot 2: Price vs Revenue
print("📊 Creating Price vs Revenue plot...")
fig2, ax2 = plt.subplots(figsize=(10, 6))

# Prepare data for swarm-visualizer
normalized_dict = {
    "Expected Revenue": {
        "x": price_simulation_range,
        "y": revenues,
        "lw": 2.5,
        "linestyle": "--",
        "color": "#fea333",  # Orange
        "alpha": 0.9,
        "zorder": 3,
    },
    "Base Price": {
        "x": [base_price, base_price],
        "y": [min(revenues), max(revenues)],
        "lw": 2,
        "linestyle": "--",
        "color": "black",
        "alpha": 0.8,
        "zorder": 2,
    },
    "Optimal Price": {
        "x": [optimal_price, optimal_price],
        "y": [min(revenues), max(revenues)],
        "lw": 2,
        "linestyle": "--",
        "color": "#2ECC71",
        "alpha": 0.8,
        "zorder": 2,
    },
}

# Use swarm-visualizer plot_overlaid_lineplot
swarm_visualizer.plot_overlaid_lineplot(
    ax=ax2,
    normalized_dict=normalized_dict,
    title_str="Price vs Revenue Optimization",
    ylabel="Expected Revenue ($)",
    xlabel="Sales Price ($)",
    legend_present=True,
)

# Use swarm-visualizer set_axis_infos for consistent styling
set_axis_infos(
    ax=ax2,
    xlabel="Sales Price ($)",
    ylabel="Expected Revenue ($)",
    title_str="Price vs Revenue Optimization",
    grid=True,
)

# Format y-axis for revenue
ax2.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, p: f"${x:,.0f}"))

plt.tight_layout()
plt.savefig("price_vs_revenue.png", dpi=300, bbox_inches="tight")
plt.show()

# Plot 3: Revenue comparison bar chart
print("📊 Creating Revenue Comparison plot...")
fig3, ax3 = plt.subplots(figsize=(8, 6))

# Create bar chart with consistent styling
bar_colors = ["black", "#51CF66"]
bars = ax3.bar(
    [
        "Base Price\n" + f"${base_price:.2f}",
        "Optimal Price\n" + f"${optimal_price:.2f}",
    ],
    [base_revenue, optimal_revenue],
    color=bar_colors,
    alpha=0.8,
    edgecolor="black",
    linewidth=2,
)

# Use swarm-visualizer set_axis_infos for consistent styling
set_axis_infos(
    ax=ax3,
    xlabel="Pricing Strategy",
    ylabel="Expected Revenue ($)",
    title_str="Revenue Comparison",
    grid=True,
)

# Add value labels on bars
for bar in bars:
    height = bar.get_height()
    ax3.text(
        bar.get_x() + bar.get_width() / 2.0,
        height,
        f"${height:,.0f}",
        ha="center",
        va="bottom",
        fontsize=11,
        fontweight="bold",
    )

# Format y-axis for revenue
ax3.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, p: f"${x:,.0f}"))

plt.tight_layout()
plt.savefig("revenue_comparison.png", dpi=300, bbox_inches="tight")
plt.show()

Next Steps

Prepare your own data with historical prices and transactions
Run the simulation with different price ranges
Analyze the results to find your optimal price point

Pro tip: Run pricing simulations regularly (monthly or quarterly) as market conditions change. Your optimal price today might not be optimal tomorrow!

Get Started

Guides

Use Cases

What is pricing simulation? How does it help?

1. Load Historical Sales Data

2: Visualize Historical Data

Example Output: Historical Data Analysis

Step 3: Set Up Pricing Simulation

Step 4: Prepare Data for Forecasting

Step 5: Run AI Forecasts

Step 6: Create Time Series Forecast Visualization

Example Output: Time Series Forecast Visualization

Step 7: Analyze Results

Step 8: Visualize Pricing Insights

Example Output: Pricing Simulation Results

Plot 1: Price vs Sales Analysis

Plot 2: Price vs Revenue Optimization

Plot 3: Revenue Comparison

Complete Code

Next Steps

​What is pricing simulation? How does it help?

​1. Load Historical Sales Data

​2: Visualize Historical Data

​Example Output: Historical Data Analysis

​Step 3: Set Up Pricing Simulation

​Step 4: Prepare Data for Forecasting

​Step 5: Run AI Forecasts

​Step 6: Create Time Series Forecast Visualization

​Example Output: Time Series Forecast Visualization

​Step 7: Analyze Results

​Step 8: Visualize Pricing Insights

​Example Output: Pricing Simulation Results

​Plot 1: Price vs Sales Analysis

​Plot 2: Price vs Revenue Optimization

​Plot 3: Revenue Comparison

​Complete Code

​Next Steps

What is pricing simulation? How does it help?

1. Load Historical Sales Data

2: Visualize Historical Data

Example Output: Historical Data Analysis

Step 3: Set Up Pricing Simulation

Step 4: Prepare Data for Forecasting

Step 5: Run AI Forecasts

Step 6: Create Time Series Forecast Visualization

Example Output: Time Series Forecast Visualization

Step 7: Analyze Results

Step 8: Visualize Pricing Insights

Example Output: Pricing Simulation Results

Plot 1: Price vs Sales Analysis

Plot 2: Price vs Revenue Optimization

Plot 3: Revenue Comparison

Complete Code

Next Steps